
Sol: The given plate is symmetrical about the y-y axis, therefore \ = 150 mm. To find \, we have to divide the whole Figure into standard areas.Įxample: Find the moment of inertia of a plate with a circular hole about its centroidal x axis as shown in Fig.8. (Note 1) I x and I y are the moments of inertia about the x- and y- axes, respectively, and are calculated by: I x y 2 dA. For example, given the axis O-O and the shaded area shown, one calculates the. The moment of inertia of the semicircle is generally expressed as I r 4 / 4.Here in order to find the value of the moment of inertia of a semicircle, we have to first derive the results of the moment of inertia full circle and basically divide it by two to get the required result of that moment of inertia for a semicircle. The second moment of area, more commonly known as the moment of inertia, I, of a cross section is an indication of a structural member's ability to resist bending.

Let us see the following figure which indicates one lamina with area A. Sol: The given I-section is symmetrical about the y-y axis, therefore, The area moment of inertia is the second moment of area around a given axis. The x and y terms inside the integral denote the centroidal position of the differential area measured from the y and x axes. Area moment of inertia is basically defined as the sum of second moment of area of individual sections about an axis. = + Įxample: Determine the moment of inertia about the horizontal axis passing through the centroid of the section as shown in Fig.7. Remember that the hole is removed from the shape, so its contribution to the total moment of inertia is negative.\\] Diameter is a straight line passing from side to side through the center of a body or figure. hence moment of inertia about the X-axis is represented by I whereas about Y-axis represents Iyy.
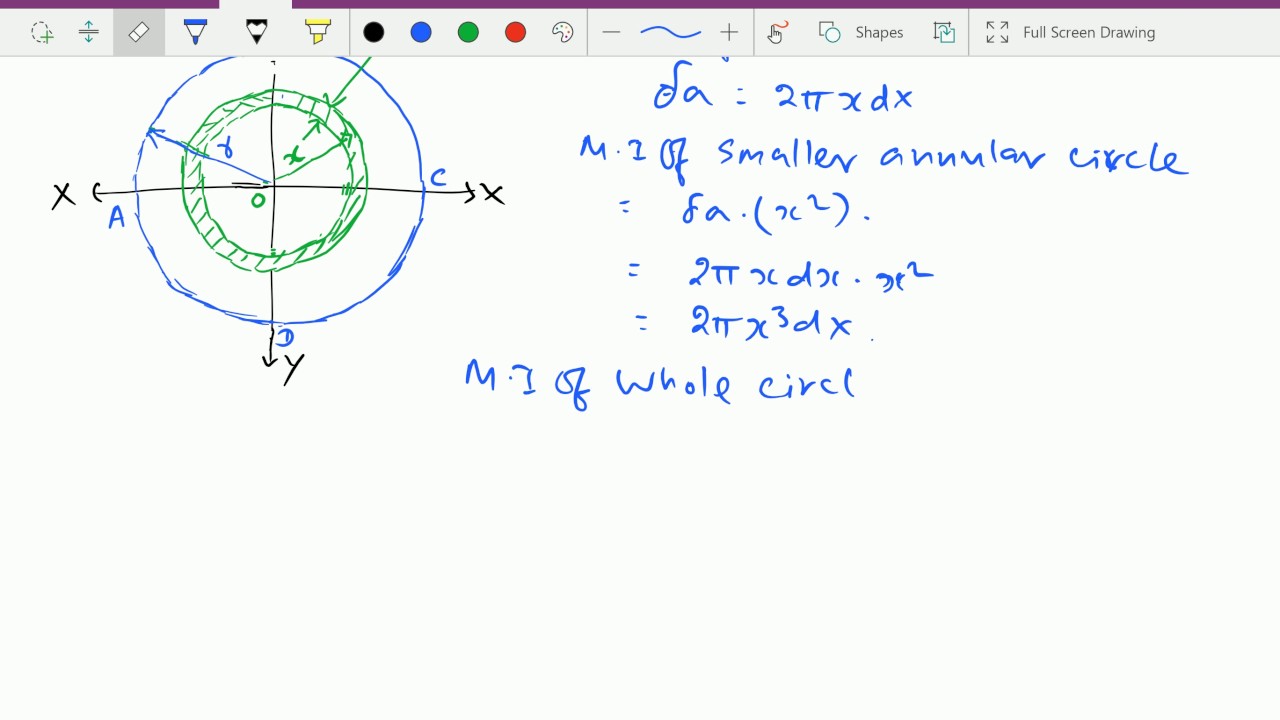
of the area ( or mass ) from an axis is called the moment of inertia of the area ( or mass ) about that axis. Organize all the necessary information into a table, then total the moments of inertia of the parts to get the moment of inertia of the whole shape. The Moment of inertia of circle about diametrical axis formula is defined as the 1/64 times of product of Archimedes' constant (pi) and diameter raised to power 4 and is represented as I (pi d 4)/64 or areamomentofinertia (pi Diameter 4)/64. The product of the area ( or mass ) and the square of the distance of the C.


 0 kommentar(er)
0 kommentar(er)
